[Java] 비트(bit)와 비트마스크(bit mask)
비트 (bit)
비트(binary digit)
: 데이터를 나타내는 최소 단위이다.
모든 데이터는 0과 1의 조합으로 구성되는데, 이 0또는 1이 하나의 비트이다. 1개의 비트는 두 가지 상태를 나타낼 수 있으므로, n비트 정수형 변수는 2^0 ~ 2^n-1까지 표현할 수 있다.
비트 연산자
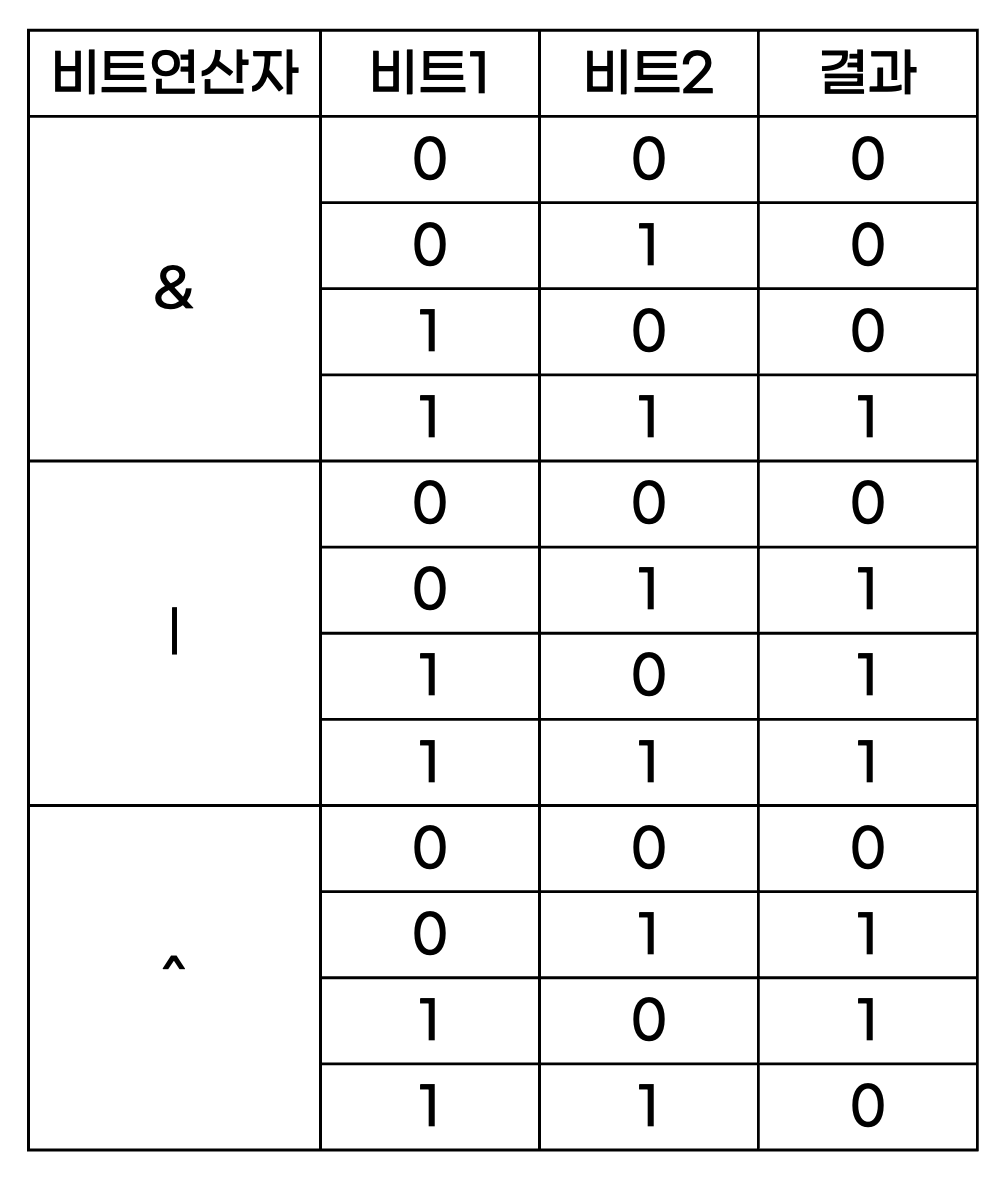
- AND 연산 (
&) : 대응하는 두 비트가 모두 1일 때 1 반환 - OR 연산 (
|) : 대응하는 두 비트 중 하나라도 1이라면 1, 아니면 0 반환 - XOR 연산 (
^) : 대응하는 두 비트가 다르면 1, 같으면 0을 반환 - NOT 연산 (
~) : 비트의 값을 반전 - Shift 연산 (
<<,>>) : 왼쪽 또는 오른쪽으로 비트를 이동
쉬프트 연산에서 중요한 점 한가지는 바로 자리수다.int는 32bit 길이를 갖지만 첫 번째 비트는 부호를 나타내는 부호 있는 정수형이기 때문에 2^31까지만 양방향으로 표현할 수 있다. 다시 말해 자료형의 범위를 정확하게 인지하지 않은 상태에서 범위를 넘어서는 쉬프트 연산을 수행할 경우 쓰레기값을 얻을 수 있다. - cf) java에서는 16bit 자료형인 char가 부호 없는(unsigned) 자료형이므로 이를 bitmask에서 많이 활용한다.
- java의 경우 int 자료형은 -2^31 ~ 2^31-1(-2147483648 ~ 2147483647) 을 범위로 갖는다.
비트마스킹
bitmask
: 정수의 이진수 표현을 자료구조로 쓰는 기법
이진 숫자로 0, 1 값을 가질 수 있고 이에 따라 true/false, on/off 와 같은 상태를 나타내는 것이 가능하다.
비트마스크 장점
- 빠른 수행시간
시간복잡도 O(1)에 구현되는 것이 많습니다. 비트마스크를 사용할 수 있다는 말은 원소의 수가 많지 않다는 뜻이기 때문에, 큰 속도 향상을 기대할 수는 없지만 여러번 수행해야 하는 경우에는 작은 최적화도 큰 속도 향상을 가져올 수 있습니다. - 간결한 코드
양한 집합 연사자들을 반복문 없이 한 줄에 쓸 수 있습니다. - 작은 메모리 사용량
적은 메모리를 사용할 수 있다는 말은 데이터를 미리 계산하여 저장해 둘 수 있으므로 캐시 효율이 좋다는 말입니다. - 연관 배열을 배열로 대체
예로 연관 배열 객체Map<Vector, int>가 있다고 합시다. 이 때 비트마스크를 이용해 정수 변수로 나타내면 단순 배열int[]로 사용할 수 있습니다.
용어 정의
비트(bit): 0과 1로 나타내는 이진수의 한 자리부호 없는 N비트 값: 20 ~ 2N-1최하위 비트(LSB): 20 에 위치한 비트최사우이 비트(MSB): 2N-1 에 위치한 비트비트가 켜져있다: 1비트가 꺼져있다: 0
비트마스크를 이용한 집합 구현
비트마스크를 이용한 집합 구현은 가장 대표적이고, 자주 쓰이는 방법이다. 하나의 bit가 하나의 데이터 상태를 의미한다. bit가 1이면 해당 원소가 집합에 포함되어 있다는 의미이고, 0이면 포함되어 있지 않다는 의미이다. 따라서, N비트는 N개의 원소를 갖는 집합의 부분집합들을 모두 표현할 수 있다.
공집합과 꽉 찬 집합 구하기
int A = 0;
A = (1 << 10) - 1;: 기본적으로 공집합은 bit가 모두 꺼진 상황이기 때문에 상수 0이 공집합을 표현한다. 반대로 꽉 찬 집합은 bit가 모두 켜진 상황이기 때문에 1111111111(2) 의 값으로 표현한다.
원소 추가
A |= (1 << k);: A 집합에 특정 원소를 추가하는 방법이다. 원소에 해당하는 bit만 켜야 하기 때문에 해당 bit를 항상 1로 만드는 연산이 필요하기 때문에 따라서 OR 연산을 이용한다.
원소 삭제
A &= ~(1 << k);: A 집합에 포함된 특정 원소를 삭제하는 방법이다. A에 k번째 원소의 포함 여부와 상관없이 해당 bit를 끄기 위해서는 AND 연산을 이용해야 한다.
1<<k: k번째가 켜진 상태^(1<<k): k번째만 꺼진 상태A &= ^(1<<k);: A 집합에 담긴 k번째 상태 off
원소의 포함 여부 확인
if((A & (1 << k)) == (1 << k)): A 집합에 특정 원소가 포함되어 있는지 확인하는 방법이다. k번째 원소가 포함되어 있는지 확인하고 싶다면, k번째 bit가 켜져 있는지만 확인하면 된다.
원소의 토글
A ^= (1 << k);: A 집합에 해당 원소가 빠져있는 경우에는 추가하고, 들어있는 경우에는 삭제하는 방법이다. XOR 연산을 이용한다.
두 집합에 대해 연산하기
A | B // A와 B의 합집합
A & B // A와 B의 교집합
A & (~B) // A에서 B를 뺀 차집합
A ^ B // A와 B중 하나에만 포함된 원소들의 집합: 두 집합을 A와 B라고 한다면 비트연산자들을 통해서 A와 B의 교집합, 합집합, 차집합 등을 구할 수 있다.
집합의 크기 구하기
int bitCount(int A){
if(A == 0) return 0;
return A%2 + bitCount(A / 2);
}
//내장 명령어
Integer.bitCount(A): 집합에 포함된 원소의 크기를 구한다면 A에서 켜진 bit의 수를 구하면 될 것이다. 직접 모든 비트를 확인하면서 개수를 체크할 수도 있고, 내장 명령어를 이용할 수도 있다.
최소 원소 찾기
int first = A & (-A);: 집합에 포함된 가장 작은 원소 (index가 가장 작은 원소)를 찾는 방법이다. 켜져 있는 bit 중에서 가장 오른쪽에 있는 bit를 찾는 것이다. 비트마스크 뿐만 아니라 펜윅 트리 (Fenwick Tree)에서도 사용되는 기법이다.
ex) 비트 A가 있다고하자.
- 가장 오른쪽에 켜져있는 bit를 k라고 하면, 0~k-1의 bit는 모두 0이다.
- 그렇다면 -A에서는 k번째 bit는 0, 0 ~ k-1의 bit는 모두 1이다.
~A + 1을 하게 되면 k번째 bit는 1, 0 ~ (k-1)의 bit는 모두 0이 된다. k이후의 비트는 아무 변화가 없다.
(~A + 1: 컴퓨터가 표현하는 A의 2의 보수 (-A) )
→ 따라서, -A와 A를 AND연산을 시키면 k번째 bit만 켜진 상태로 남게 된다.
ex) int first = A & (-A);
A : 1010,
~A+1 (-A) : 0110,
A&(-A) : 0010
최소 원소 지우기
A &= (A - 1);: 가장 오른쪽에 켜져 있는 bit를 지우고 싶다면 A-1과 AND시키면 된다. A에서 1을 빼주게 되면 가장 오른쪽에 있던 bit는 0이 되고 그보다 오른쪽에 있는 모든 bit들이 1이 되기 때문이다.
ex) A &= (A - 1);
A : 1010,
A-1 : 1001,
A&(A-1) : 1000
Reference